트리

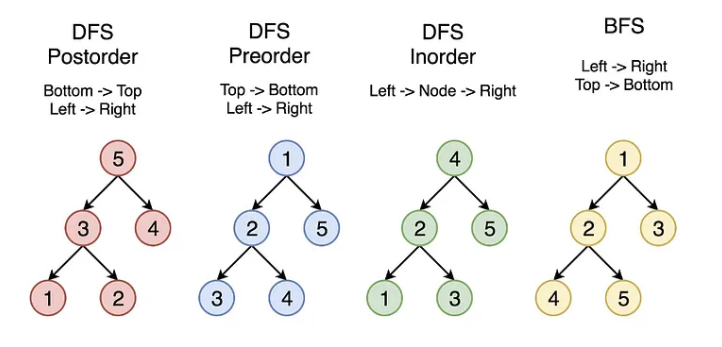
이진 트리
1. maximum-depth-of-binary-tree
문제 : https://leetcode.com/problems/maximum-depth-of-binary-tree/
트리의 깊이를 찾는 문제다.
먼저 DFS 방식으로 풀 수 있다.
n : 노드의 갯수, h : 트리의 최대 깊이
시간 복잡도 : O(n) -> 모든 노드를 한번씩 방문
공강 복잡도 : O(h) -> 재귀 콜 스택에 최대 h개의 노드
fun maxDepth(root: TreeNode?): Int {
if(root == null) return 0
var left = maxDepth(root.left)
var right = maxDepth(root.right)
return maxOf(left, right) +1
}
BFS 방식으로도 풀 수 있다.
n : 노드의 갯수, w: 최대 넓이
시간 복잡도 : O(n) -> 모든 노드를 한번씩 방문
공강 복잡도 : O(w) -> 최악의 경우 큐에 가장 넓은 레벨의 모든 노드가 들어감
fun maxDepth(root: TreeNode?): Int {
if(root == null) return 0
val queue: Queue<TreeNode> = LinkedList()
queue.offer(root)
var depth = 0
while(queue.isNotEmpty()) {
val size = queue.size
depth ++
repeat(size) {
val node = queue.poll()
node.left?.let{queue.offer(it)}
node.right?.let{queue.offer(it)}
}
}
return depth
}
참고 )
1. 완전 이진 트리 (balanced)
- 노드 수 n = 2^h - 1 → 균형 잡힘
- DFS 공간: O(log n)
- BFS 공간: O(n/2) (마지막 레벨이 큐에 들어감)
- 시간은 둘 다 O(n)
- 공간은 트리 구조에 따라 DFS가 더 유리하거나 불리할 수 있음
- 균형 트리라면 DFS는 더 메모리 효율적
- BFS는 모든 레벨을 동시에 보기에 **레벨 기반 문제(예: 최소 깊이)**에 더 적합
2. same-tree
문제 : https://leetcode.com/problems/same-tree/
두개의 트리가 같은지 물어보는 문제다.
DFS 방법
fun isSameTree(p: TreeNode?, q: TreeNode?): Boolean {
if(p == null && q == null) {
return true
}
if(p == null || q== null ) {
return false
}
if(p.`val` != q.`val`) {
return false
}
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right)
}
BFS 방법
fun isSameTree(p: TreeNode?, q: TreeNode?): Boolean {
if(p == null && q == null) {
return true
}
if(p == null || q== null ) {
return false
}
val pQueue:Queue<TreeNode> = LinkedList()
val qQueue:Queue<TreeNode> = LinkedList()
pQueue.offer(p)
qQueue.offer(q)
while(pQueue.isNotEmpty() && qQueue.isNotEmpty()) {
val pTemp = pQueue.poll()
val qTemp = qQueue.poll()
if(pTemp == null && qTemp == null) continue
if(pTemp == null || qTemp == null) return false
if(pTemp.`val` != qTemp.`val`) return false
pQueue.offer(pTemp.left)
pQueue.offer(pTemp.right)
qQueue.offer(qTemp.left)
qQueue.offer(qTemp.right)
}
return pQueue.isEmpty() && qQueue.isEmpty()
}
3. 트리 뒤집기
문제 : https://leetcode.com/problems/invert-binary-tree/
주어진 트리의 좌우를 바꾸는 문제이다.
DFS
fun invertTree(root: TreeNode?): TreeNode? {
if(root == null) {
return null
}
val left = invertTree(root.left)
val right = invertTree(root.right)
root.right = left
root.left = right
return root
}
BFS
fun invertTree(root: TreeNode?): TreeNode? {
if(root == null) return null
val queue: Queue<TreeNode> = LinkedList()
queue.offer(root)
while(queue.isNotEmpty()) {
val node = queue.poll()
val temp = node.left
node.left = node.right
node.right = temp
node.left?.let{queue.offer(it)}
node.right?.let{queue.offer(it)}
}
return root
}
4. 트리의 최대합 구하기
문제 : https://leetcode.com/problems/binary-tree-maximum-path-sum/submissions/1633699245/
현재 노드까지의 최대 합을 구하고 갱신해서 최댓값을 구하는 방식으로 DFS로 문제를 풀수 있다.
BFS방식은 모든 노드를 방문해서 레벨 순서로 순회하고, 현재 노드와 자식들을 보고 지나가기 때문에, 노드 기준으로 양쪽 자식을 더해서 구성하는 판단이 불가능하다.
✅ BFS로 가능한 범위
| 문제 종류 | DFS 적합 | BFS 가능 |
| 최대 깊이 (maxDepth) | ✅ | ✅ |
| 최소 깊이 (minDepth) | ✅ | ✅ |
| 루트→리프 경로합 (hasPathSum) | ✅ | ✅ |
| 🔥 임의의 경로에서 최대 합 (maxPathSum) | ✅ | ❌ |
class Solution {
var maxSum = Int.MIN_VALUE
fun maxPathSum(root: TreeNode?): Int {
dfs(root)
return maxSum
}
fun dfs(root: TreeNode?): Int {
if(root == null) {
return 0
}
val left = maxOf(0, dfs(root.left))
val right = maxOf(0, dfs(root.right))
val temp = root.`val` + right + left
maxSum = maxOf(maxSum, temp)
return root.`val` + maxOf(right, left)
}
}
5. Binary Tree Level Order Traversal
문제 : https://leetcode.com/problems/binary-tree-level-order-traversal/
이진 트리의 레벨 별 리스트를 구하는 문제이다.
BFS 방식을 이용하면 직관적으로 풀 수 있다.
BFS를 이용한 방식으로 문제를 풀었다.
class Solution {
fun levelOrder(root: TreeNode?): List<List<Int>> {
if (root == null) {
return emptyList()
}
val answer = mutableListOf<MutableList<Int>>()
val queue: Queue<Pair<TreeNode, Int>> = LinkedList()
queue.offer(Pair(root, 0))
while(queue.isNotEmpty()) {
val (node, level) = queue.poll()
if(level == answer.size) {
answer.add(mutableListOf())
}
answer[level].add(node.`val`)
node.left?.let{queue.offer(Pair(it, level + 1))}
node.right?.let{queue.offer(Pair(it, level + 1))}
}
return answer
}
}
DFS 방식을 사용하면 더 간단하게 풀 수 있다.
DFS로는 다음과 같이 풀 수 있다.
fun levelOrder(root: TreeNode?): List<List<Int>> {
val result = mutableListOf<MutableList<Int>>()
dfs(root, 0, result)
return result
}
fun dfs(root:TreeNode?, level:Int, result: MutableList<MutableList<Int>>) {
if(root == null) return
if(result.size == level) {
result.add(mutableListOf())
}
result[level].add(root.`val`)
dfs(root.left, level+1, result)
dfs(root.right, level+1, result)
}
6. Serialize and Deserialize Binary Tree
트리를 인코딩하고 디코딩 하는 문제이다.
BFS를 사용하면 다음과 같다.
class Codec() {
// Encodes a URL to a shortened URL.
fun serialize(root: TreeNode?): String {
if(root == null) return "null"
val queue :Queue<TreeNode> = LinkedList()
val result = mutableListOf<String>()
queue.offer(root)
while(queue.isNotEmpty()) {
val node = queue.poll()
if(node == null ) {
result.add("null")
}else {
result.add(node.`val`.toString())
queue.offer(node.left)
queue.offer(node.right)
}
}
return result.joinToString(",")
}
// Decodes your encoded data to tree.
fun deserialize(data: String): TreeNode? {
if(data == "null") return null
val values = data.split(",")
val root = TreeNode(values[0].toInt())
val queue: Queue<TreeNode> = LinkedList()
queue.offer(root)
var i = 1
while (queue.isNotEmpty() && i < values.size) {
val current = queue.poll()
if(values[i] != "null") {
val left = TreeNode(values[i].toInt())
current.left = left
queue.offer(left)
}
i ++
if(i<values.size && values[i] != "null") {
val right = TreeNode(values[i].toInt())
current.right = right
queue.offer(right)
}
i++
}
return root
}
}
DFS로 풀면 다음과 같다.
fun serialize(root:TreeNode?): String {
val sb = StringBuilder()
fun dfs(node: TreeNode?) {
if (node == null) {
sb.append("null,")
return
}
sb.append("${node.`val`},")
dfs(node.left)
dfs(node.right)
}
dfs(root)
return sb.toString()
}
fun deserialize(data: String): TreeNode? {
val nodes = LinkedList(data.split(",").toList())
fun dfs(): TreeNode? {
val value = nodes.poll()
if(value == "null") return null
val node = TreeNode(value.toInt())
node.left = dfs()
node.right = dfs()
return node
}
return dfs()
}
7. Kth Smallest Element
문제 : https://leetcode.com/problems/kth-smallest-element-in-a-bst/
BST에서 k번째로 작은 수를 찾는 문제이다.
처음에는 BST라고 생각을 안하고 넓이 우선 탐색으로 전체 탐색하고 정렬해서 문제를 풀었다.
fun kthSmallest(root: TreeNode?, k: Int): Int {
// 모든 트리를 순회하면서 정렬하기
if(root == null || k == 0) return 0
val answer = mutableListOf<Int>()
val queue: Queue<TreeNode> = LinkedList()
queue.offer(root)
while(queue.isNotEmpty()) {
val node = queue.poll()
answer.add(node.`val`)
node.left?.let{queue.offer(it)}
node.right?.let{queue.offer(it)}
}
answer.sort()
return answer[k-1]
}
하지만 해당 문제는 이렇게 풀면 안된다.
문제에서 BST로 주어졌는데, 이진 트리 탐색의 경우 다음과 같은 특징을 가진다.
중위 순회의 경우 순차 정렬된다. (Inorder Traversal을 수행하여 모든 키를 정렬된 순서)
참고 :https://yoongrammer.tistory.com/71
[자료구조] 이진 탐색 트리 (BST, Binary Search Tree)
목차이진 탐색 트리 (BST, Binary Search Tree)이진 탐색 트리란 정렬된 이진트리로써 다음과 같은 속성을 가지고 있습니다.노드의 왼쪽 하위 트리에는 노드의 키보다 작은 키가있는 노드 만 포함됩니
yoongrammer.tistory.com
이를 이용해서 문제를 다시푼다.
H = 트리높이라고할때,
시간 복잡도 (H + K)이다.
최악의 경우 (불균형트리) -> O(N),
균형잡힌 트리인경우 -> O(logN + K)
private var count = 0
private var result = 0
fun kthSmallest(root: TreeNode?, k: Int): Int {
if(root == null || k == 0) return 0
inorder(root, k)
return result
}
private fun inorder(node: TreeNode?, k: Int) {
if(node == null) {
return
}
inorder(node.left, k)
count ++
if (count == k) {
result = node.`val`
return
}
inorder(node.right, k)
}
8. Lowest common ancestor of BST
문제 : https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/
두개의 노드가 주어지면 공통 부모 노드중에서 가장 최소 부모를 찾는 문제이다.
BST에서는 해당 노드보다 작으면 왼쪽, 크면 오른쪽에 위치하게 된다는 점을 활용해야한다.
왼쪽 노드 < 현재 노드 < 오른쪽 노드
즉, 노드가 p, q의 공통 조상이 되려면 다음중 하나여야 한다.
- p와 q가 양쪽 자식에 하나씩 있음 (즉, p < node < q 또는 q < node < p)
- p 또는 q가 node 자신임 (자기 자신도 조상이 될 수 있음)
시간복잡도 O(h)
공간복잡도 O(n)
- 재귀 호출 스택 사용
으로 문제를 풀 수 있다.
class Solution {
fun lowestCommonAncestor(root: TreeNode?, p: TreeNode?, q: TreeNode?): TreeNode? {
val value = root?.`val` ?: return null
val pVal = p?.`val` ?: return null
val qVal = q?.`val` ?: return null
return when {
pVal < value && qVal < value -> lowestCommonAncestor(root.left, p, q)
pVal >value && qVal > value -> lowestCommonAncestor(root.right, p, q)
else -> root
}
}
}
반복문으로도 해당 문제를 풀 수 있다.
명시적 재귀 호출이 없고 node 하나만의 참조만으로 루프를 돌아서 스택도 안 쓰고, 함수 호출도 한 번이므로 공간은 상수이다.
반복문의 경우 공간 복잡도가 O(1)로 줄어든다 .
fun lowestCommonAncestor(root: TreeNode?, p: TreeNode?, q: TreeNode?): TreeNode? {
var node = root
if(q == null || p == null){
return null
}
while (node != null) {
val value = node.`val`
when {
p.`val`<value && q.`val`< value -> node = node.left
p.`val`>value && q.`val`> value -> node = node.right
else -> return node
}
}
return null
}
9. Implement Trie (Prefix Tree)
문제 : https://leetcode.com/problems/implement-trie-prefix-tree/
트리를 실제로 구현하는 문제로, 다음과 같이 풀 수 있다.
트리를 구성할 때, 시작점을 잡고 새로운 단어가 추가될때마다 시작점으로 부터 자식을 추가할 수 있다.
만약에, app, apple, bat이라는 단어를 추가하면 다음과 같은 구조가 된다.
- n: 단어의 수
- L: 단어 하나의 최대 길이 (즉, 입력 문자열의 길이)
- Σ: 알파벳 수 (보통 26 for lowercase 영어 알파벳)
insert의 경우시간
시간 복잡도 O(L)
- 각 문자를 하나씩 순회하면서 노드를 따라가거나 새로 생성
- 최악의 경우 루트부터 리프까지 L개의 노드를 방문하거나 생성
공간복잡도는 O(L)
- 새로운 문자가 등장할 때마다 새로운 TrieNode가 생성
- 따라서 한 단어에 대해 최대 L개의 노드가 추가
- 전체적으로 n개의 서로 다른 단어가 겹치는 부분 없이 삽입되면 총 O(n·L) 개의 노드가 생길 수 있음
search의 경우
시간 복잡도: O(L)
- 문자를 하나씩 따라가며 자식 노드를 탐색
- TrieNode는 Map<Char, TrieNode> 구조이므로 각 문자는 O(1)에 탐색 가능
공간 복잡도: O(1)
- 새로운 데이터를 저장하거나 생성하지 않기 때문에 상수 공간 사용
startsWith의 경우
시간 복잡도: O(L)
- prefix의 길이만큼 문자들을 따라 내려가며 확인
공간 복잡도: O(1)
- search와 동일하게 새로운 데이터 생성 없음
(root)
├── 'a'
│ └── 'p'
│ └── 'p'* (for "app")
│ └── 'l'
│ └── 'e'* (for "apple")
└── 'b'
└── 'a'
└── 't'* (for "bat")
class TrieNode() {
val children = mutableMapOf<Char, TrieNode>()
var isWord = false
}
class Trie() {
private val root = TrieNode()
fun insert(word: String) {
var node = root
for (char in word) {
node = node.children.getOrPut(char) {TrieNode()}
}
node.isWord = true
}
fun search(word: String): Boolean {
val node = findNode(word)
return node != null && node.isWord
}
fun startsWith(prefix: String): Boolean {
return findNode(prefix) != null
}
private fun findNode(prefix: String): TrieNode? {
var node = root
for (char in prefix) {
node = node.children[char] ?: return null
}
return node
}
}
10. Add and Search Word
문제 : https://leetcode.com/problems/design-add-and-search-words-data-structure/
위의 트리 insert, search 문제에 와일드 카드 개념의 '.' 가 추가된 문제이다.
와일드 카드가 사용되는 경우 하위의 모든 케이스를 백트래킹 해야 하므로 Trei + DFS 개념이 추가되었다.
addWord의 경우
시간 복잡도 O(L)
- 각 문자를 하나씩 순회하면서 노드를 따라가거나 새로 생성
- 최악의 경우 루트부터 리프까지 L개의 노드를 방문하거나 생성
공간복잡도는 O(L)
- 새로운 문자가 등장할 때마다 새로운 TrieNode가 생성
- 따라서 한 단어에 대해 최대 L개의 노드가 추가
- 전체적으로 n개의 서로 다른 단어가 겹치는 부분 없이 삽입되면 총 O(n·L) 개의 노드가 생길 수 있음
search의 경우
시간 복잡도는 일반적인 경우 O(L)
최악의 경우 시간 복잡도: O(26^d * L)
- d: 검색 문자열 내의 '.' 개수 (DFS 분기 수)
- L: 전체 단어 길이
- 왜냐하면:
- 각 .는 최대 26개의 분기로 나뉘며,
- 모든 경로마다 최대 L번 DFS가 일어날 수 있음
공간 복잡도는 O(L)
- 스택 깊이
class Word() {
val children = mutableMapOf<Char, Word>()
var isWord = false
}
class WordDictionary() {
private val root = Word()
fun addWord(word: String) {
var node = root
for (char in word) {
node = node.children.getOrPut(char){ Word()}
}
node.isWord = true
}
fun search(word: String): Boolean {
return findWord(word, 0, root)
}
private fun findWord(word: String, index: Int, node: Word): Boolean {
if (index == word.length) return node.isWord
var char = word[index]
if(char == '.') {
for (child in node.children.values) {
if(findWord(word, index+1, child))return true
}
return false
} else {
val next = node.children[char] ?: return false
return findWord(word, index+1, next)
}
}
}
11. Word Search 2
문제 : https://leetcode.com/problems/word-search-ii/submissions/1638358383/
board: 2D 문자 격자 (n x m), words: 단어 리스트가 주어지고 board 내에서 단어를 찾되, 상하좌우 인접한 문자로만 이동 가능한 문제다. 단, 동일한 셀은 한 단어에서 한 번만 사용 가능하다.
다음의 순서로 문제를 풀 수 있다.
- Trie로 모든 단어 저장
→ 접두어 단위로 pruning(가지치기) 할 수 있음 - DFS로 board를 순회하면서 Trie와 동시에 탐색
→ 매 DFS 경로는 Trie의 한 경로에 대응되며, isEnd이면 정답
시간 복잡도는 다음과 같다.
- W = 단어 수
- L = 평균 단어 길이
- M × N = board 크기
O(W × L) + O(M × N × 4^L)
- Trie 구성: O(W * L)
- W = 단어 수, L = 평균 단어 길이
- DFS 탐색: O(M * N * 4^L)
- M x N board의 모든 셀에서 길이 L까지 백트래킹
- Trie로 pruning 되므로 실제 탐색 공간은 훨씬 작음
공간복잡도는 다음과 같다.
O(W × L + L) = O(W × L)
- Trie 노드: O(W * L)
- DFS 스택: O(L) (백트래킹 깊이)
class Solution {
class TrieNode() {
val children = mutableMapOf<Char, TrieNode>()
var word: String? = null
}
fun findWords(board: Array<CharArray>, words: Array<String>): List<String> {
val result = mutableListOf<String>()
val root = buildTrie(words)
val rows = board.size
val cols = board[0].size
for (r in 0 until rows) {
for (c in 0 until cols) {
dfs(board, r, c, root, result)
}
}
return result
}
private fun dfs(
board: Array<CharArray>,
r: Int,
c: Int,
node: TrieNode,
result: MutableList<String>
) {
// 범위를 벗어나거나 이미 방문한 경우
if( r !in board.indices || c!in board[0].indices || board[r][c] == '#') return
val char = board[r][c]
val nextNode = node.children[char] ?: return
// 단어완성
nextNode.word?.let {
result.add(it)
nextNode.word = null // 중복 방지
}
// 방문 표시
board[r][c] = '#'
// 상하 좌우
dfs(board, r-1, c, nextNode, result)
dfs(board, r+1, c, nextNode, result)
dfs(board, r, c-1, nextNode, result)
dfs(board, r, c+1, nextNode, result)
// 복구
board[r][c]= char
}
private fun buildTrie(words:Array<String>) : TrieNode{
val root = TrieNode()
for (word in words) {
var node = root
for (char in word) {
node = node.children.getOrPut(char) {TrieNode()}
}
node.word = word
}
return root
}
}